Halo sobat semua. Dalam artikel kali ini, saya ingin berbagi tentang cara menuliskan dan menyelesaikan persamaan matematis dengan menggunakan MATLAB. MATLAB tak
hanya populer karena kemampuan visualisasi 2D dan 3Dnya, tetapi juga dikenal
dalam hal komputasi matematis termasuk di dalamnya penyelesaian sistem
persamaan. Penyelesaian sistem persamaan baik berupa persamaan aljabar
sederhana hingga yang tingkat tinggi dilakukan oleh MATLAB dengan komputasi
variabel simbolik. Perintah atau fungsi komputasi ini dalam MATLAB disediakan
melalui fitur Symbolic Math Toolbox.
Pada bagian ini akan dibahas tentang penyelesaian sistem persamaan aljabar
sederhana, kuadrat, hingga persamaan logaritma dan eksponen.
Persamaan Aljabar Sederhana
Persamaan
aljabar sederhana adalah suatu persamaan yang memuat satu atau lebih variabel
dengan pangkat tertingginya satu. Untuk menyelesaikan persamaan aljabar
sederhana hingga kompleks dengan menggunakan MATLAB, kita dapat menggunakan
perintah solve. Perintah ini biasanya didahului
dengan mendeklarasikan variabel simbolik melalui ekspresi perintah syms.
solve(eqn,var):
menyelesaikan suatu persamaan dengan variabel tertentu.
Contoh 1
a. Menentukan
nilai x yang memenuhi x + 3 = 10.
Pada jendela perintah, tuliskanlah sintaks berikut.
>> syms x %membuat variabel simbolik x
>> solve(x+3==10,x)
ans =
7
b. Menentukan nilai x yang memenuhi 5x + 7 = 37
>>
syms x
>> solve (5*x + 7
== 37,x)
ans =
6
c. Menentukan nilai x yang memenuhi sin(x) = 1.
>> syms x
>> solve(sin(x)==1,x)
ans =
pi/2
d. Menentukan nilai x yang memenuhi ax + 7 = 10.
>>
syms a x %membuat variabel simbolik a dan x
>>
solve(a*x+7==10,x)
ans =
3/a
e. Menentukan nilai a yang memenuhi ax + 7 = 10.
>>
syms a x
>> solve(a*x+7==10,a)
ans =
3/x
Persamaan Kuadrat
Persamaan kuadrat atau persamaan pangkat dua adalah
persamaan dengan pangkat tertinggi variabelnya adalah dua. Penyelesaian dari
suatu persamaan kuadrat biasa disebut dengan akar-akar persamaan kuadrat.
Adapun bentuk umum persamaan kuadrat dapat dituliskan sebagai berikut:
ax2 + bx + c = 0, dengan a,
b, c
R dan a
0
Perhatikanlah
cara menyelesaikan persamaan kuadrat dengan menggunakan MATLAB berikut ini.
Contoh 1
Menentukan nilai x yang memenuhi x2+x-6=0.
a. >> syms x
>> solve(x^2+x-6==0,x)
ans =
-3
2
Jadi, nilai x yang memenuhi adalah {-3,2}.
MATLAB juga
menyediakan perintah fplot yang dapat kita gunakan untuk
membuat plot grafik suatu fungsi. Bentuk grafik dari persamaan kuadrat adalah
kurva non-linear atau lengkung.
b. >> syms x
%menggunakan
fplot untuk memplot grafik fungsi
>>fplot(x^2+x-6);xlabel('sumbu-x');ylabel('sumbu-y');grid
on
Dari plot di atas dapat diamati bahwa nilai-nilai
fungsi (y) bernilai 0 (y = 0) terjadi pada saat x = {-3,2} yang merupakan
akar-akar atau solusi persamaan kuadrat
x2+x-6 = 0.
Contoh 2
a. Menentukan nilai x yang memenuhi 3x2 +11x-4=0.
>> syms x
>> solve(3*x^2 - 11*x - 4==0,x)
ans =
-1/3
4
Jadi, nilai x yang memenuhi adalah {-1/3,4}.
b. Menentukan nilai x yang memenuhi 15x2 +2x-8=0.
>>
syms x
>> solve(15*x^2 +
2*x - 8==0,x)
ans =
-4/5
2/3
Jadi, nilai x yang memenuhi adalah {-4/5,2/3}.
Contoh 3
Menentukan nilai x yang memenuhi
a. >> syms x
>>
solve(x^2+2*x-3^(1/2)==0,x)
ans
=
(3^(1/2)
+ 1)^(1/2) - 1
-(3^(1/2)
+ 1)^(1/2) – 1
%menampilkan
hasil dengan format bilangan desimal
>>
double(ans)
ans =
0.6529
-2.6529
Jadi, nilai x yang memenuhi adalah {-2,653; 0,653}.
b. >> syms x
>>fplot(x^2+2*x-3^(1/2));xlabel('sumbu-x');
ylabel('sumbu-y');grid on
Berbeda halnya dengan persamaan sederhana, suatu
persamaan dikatakan persamaan tingkat tinggi apabila variabelnya berpangkat
lebih dari dua. Persamaan ini biasa juga dikenal dengan persamaan suku banyak
(polinomial) atau persamaan berderajat tinggi. Misalnya, suatu persamaan dengan
pangkat tertinggi 5 disebut persamaan atau polinomial berderajat 5. Grafik dari
persamaan tingkat tinggi adalah berupa kurva non-linear. Berikut ini disajikan
beberapa contoh penyelesaian persamaan tingkat tinggi dengan MATLAB.
Contoh 1
a.
Menentukan nilai x yang memenuhi (2x+1)2(x+5) = 0.
>>
syms x
>>
solve((2*x+1)^2*(x+5)==0,x)
ans =
-5
-1/2
-1/2
Jadi, nilai x yang memenuhi adalah {-5,-1/2}.
b. Menentukan nilai x yang
memenuhi x3-4x2-7x+10=0.
>>
syms x
>> solve(x^3-4*x^2-7*x+10==0,x)
ans =
-2
1
5
Jadi, nilai x yang memenuhi adalah {-2,1,5}.
Apabila
fungsi di atas diplot menggunakan fplot maka akan diperoleh hasil berikut.
>>
syms x
>>fplot(x^3-4*x^2-7*x+10);xlabel('sumbu-x');
ylabel('sumbu-y'); grid on
 |
| Plot fungsi x3-4x2-7x+10=0 |
Contoh 2
a.
Menentukan nilai x yang memenuhi x4+4x3-3x2-10x+8=0.
>> syms x
>>
solve(x^4+4*x^3-3*x^2-10*x+8==0,x)
ans =
-4
-2
1
1
Jadi, nilai x yang memenuhi adalah {-4,-2,1}.
b. >> syms x
>> fplot(x^4+4*x^3-3*x^2-10*x+8);xlabel('sumbu-x'); ylabel('sumbu-y');grid
on
 |
| Plot fungsi x4+4x3-3x2-10x+8=0 |
Sistem Persamaan Linear Multivariabel
Sistem persamaan linear (SPL) multivariabel terdiri
dari beberapa persamaan dengan dua atau lebih variabel dimana pangkat
tertingginya satu. Kata sistem merujuk pada pengertian bahwa
persamaan-persamaan tersebut perlu dipertimbangkan bersama-sama untuk mencari
solusi yang memenuhi. Berikut ini diberikan beberapa contoh penyelesaian SPL
multivariabel dengan menggunakan perintah solve dan linsolve pada MATLAB.
Contoh 1
Menentukan nilai x dan
y yang memenuhi persamaan linear dua variabel berikut:
>> syms x y %membuat variabel simbolik x dan y
>> S = solve([x+2*y==-1,4*x-3*y==18],[x,y])
S =
x: [1x1 sym]
y: [1x1 sym]
>> S.x %menampilkan nilai x
ans =
3
>> S.y %menampilkan nilai y
ans =
-2
Jadi, nilai x = 3
dan y = -2.
Contoh 2
Menentukan nilai x dan
y yang memenuhi persamaan linear dua variabel berikut:
>>
syms x y
>>
S = solve([1/(x+y)==5/27,1/(2*x-y)==2/33],[x,y]);
>> S.x
ans =
73/10
>> S.y
ans =
-19/10
Jadi, nilai x =
73/10 dan y = -19/10.
Contoh 3
Menentukan nilai x, y
dan z yang memenuhi persamaan linear tiga variabel berikut:
>>
syms x y z
>>
S = solve([x-3*y+2*z==8,2*x+y-2*z==0,3*x+5*y-z==17],[x,y,z]);
>> S.x %menampilkan nilai x
ans =
4
>> S.y %menampilkan nilai y
ans =
2
>> S.z %menampilkan nilai z
ans =
5
Jadi, nilai x = 4,
y = 2, dan z = 5.
Selain cara penyelesaian menggunakan solve, terdapat cara lain yang dapat digunakan untuk mencari solusi
sistem persamaan linear, yaitu dengan perintah linsolve.
X
= linsolve(A,B):
mencari solusi sistem persamaan linear (X) yang dinyatakan dalam bentuk matriks
AX=B, dimana B merupakan vektor kolom.
Contoh 4
Tentukan
nilai x, y dan z yang memenuhi persamaan linear tiga variabel berikut:
Untuk menyelesaikannya,
ketiklah sintaks berikut pada jendela editor.
A=[1 -3 2;
2 1
-2;
3 5
-1];
B = [8;0;17];
X=linsolve(A,B)
Apabila program di atas dieksekusi,
maka akan ditampilkan hasil:
X =
4.0000
2.0000
5.0000
Jadi, nilai x = 4,
y = 2, dan z = 5.
Contoh 5
Menentukan nilai p, q, r dan s yang
memenuhi persamaan linear multivariabel berikut:
>>
syms p q r s
>>
S = solve([2*p+3*q+r+s==12,p+q+5*r s==15,3*p+2*q+2*r+4*s==9,…
4*p-q+3*r+2*s==5],[p,q,r,s]);
>> S.p %menampilkan
nilai p
ans =
1
>> S.q %menampilkan nilai q
ans =
3
>> S.r %menampilkan nilai r
ans =
2
>> S.s %menampilkan nilai s
ans =
-1
Jadi, nilai p = 1,
q = 3, r = 2, dan s = -1.
Persamaan Logaritma dan Eksponen
Selain sistem persamaan linear multivariabel,
perintah solve yang terdapat dalam MATLAB dapat
pula digunakan untuk menyelesaikan persamaan logaritma dan eksponen atau
perpangkatan. Perhatikanlah
contoh-contohnya di bawah ini.
Contoh 1
Menentukan
nilai x yang memenuhi
.
>> syms x
>> solve(log10(x)-log10(x+5)==1,x)
ans =
-50/9
Jadi, nilai x =
-50/9.
Contoh 2
Menentukan nilai x yang
memenuhi
>> syms x
>> solve(2^(2*x)==10,x)
ans =
log(10)/(2*log(2))
%menampilkan hasil dengan format bilangan desimal
>> double(ans)
ans =
1.6610
Jadi, nilai x =
1,661
Contoh 3
Menentukan nilai-nilai
x dan y yang memenuhi persamaan eksponen:
>>
syms x
>>
S = solve([5^(x-2*y+1)==25^(x-2*y),4^(x-y+2)==32^(x-2*y+1)],[x,y])
>> S.x
ans =
5.0
>> S.y
ans =
2.0
Jadi, nilai x = 5
dan y = 2.
Demikianlah pembahasan tentang cara menuliskan dan menyelesaikan persamaan matematis dengan menggunakan MATLAB. Nantikan artikel menarik lainnya seputar pemrograman MATLAB. Semoga bermanfaat.😊






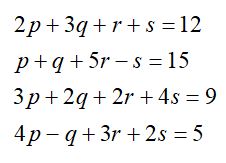

Tidak ada komentar:
Posting Komentar