a. Titik, Garis, dan Bidang
Titik dinyatakan
dengan sebuah noktah kecil dan diberi nama dengan satu huruf kapital seperti A,
B, C dan lain-lain. Kumpulan titik-titik yang teratur akan membentuk garis.
Garis digambarkan melalui segmen garis saja karena terbatasnya ruang gambar.
Garis biasanya diberi nama dengan satu huruf kecil misalnya garis
l, m, atau n
Bidang mempunyai
dua dimensi yaitu panjang dan lebar. Terdapat dua macam bidang yaitu bidang
datar dan bidang lengkung. Bidang yang akan dibahas disini adalah bidang datar.
Bidang biasanya diberi nama dengan huruf kecil dari abjad Yunani seperti α, β, γ, atau δ.
b. Kedudukan Titik terhadap Garis
Ada dua
kemungkinan kedudukan titik terhadap garis yaitu titik yang terletak pada garis
atau titik yang terletak di luar garis.
1. Titik
A dikatakan terletak pada garis l jika titik tersebut dapat dilalui oleh garis l atau perpanjangannya.
2. Titik
A dikatakan terletak di luar garis l jika titik tersebut tidak dapat dilalui oleh
garis l atau perpanjangannya.
 |
| sumber: partnermatematika.com |
c. Kedudukan Titik terhadap Bidang
Ada dua
kemungkinan kedudukan titik terhadap bidang yaitu titik yang terletak pada
bidang atau titik yang terletak di luar bidang.
1. Titik
A dikatakan terletak pada bidang α jika titik tersebut dapat dilalui oleh bidang α atau perluasannya.
2. Titik
A dikatakan terletak di luar bidang α jika titik tersebut tidak dapat dilalui oleh
bidang α atau perluasannya.
 |
| sumber: partnermatematika.com |
d. Kedudukan Garis terhadap Garis
Terdapat empat
kemungkinan kedudukan antara dua garis di dalam ruang yaitu:
1. Dua
garis sejajar, jika kedua garis itu terletak pada satu bidang dan titik
memiliki titik potong atau titik persekutuan.
2. Dua
garis berimpit, jika kedua garis tersebut mempunyai paling sedikit dua titik
persekutuan.
3. Dua
garis berpotongan, jika kedua garis itu mempunyai satu titik potong.
4. Dua
garis bersilangan, jika kedua garis tidak terletak pada satu bidang dan kedua
garis tidak sejajar ataupun berpotongan.
 |
| sumber: studiobelajar.com |
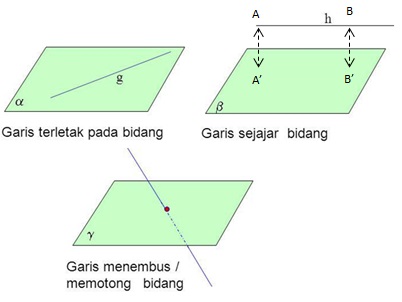
e. Kedudukan Garis terhadap Bidang
Ada tiga
kemungkinan kedudukan garis terhadap bidang yaitu garis terletak pada bidang,
garis sejajar bidang dan garis menembus bidang.
1. Garis terletak
pada bidang jika terdapat minimal dua buah titik persekutuan yang terletak pada
garis dan juga pada bidang.
2. Garis sejajar
bidang jika garis dan bidang tidak mempunyai titik persekutuan walaupun
garisnya diperpanjang dan bidangnya diperluas.
3. Garis menembus
bidang jika dan hanya jika terdapat satu titik persekutuan (titik tembus)
antara garis dan bidang.
 |
| sumber: partnermatematika.com |
f. Kedudukan Bidang terhadap Bidang
Kedudukan bidang
terhadap bidang lainnya yang mungkin terjadi adalah:
1. Jika
kedua bidang itu mempunyai tiga buah titik persekutuan yang tidak segaris maka
dua bidang dikatakan berimpit.
2. Jika
kedua bidang itu tidak mempunyai titik persekutuan walaupun diperluas maka kedua
bidang dikatakan sejajar.
3. Jika
kedua bidang itu tidak berimpit maupun sejajar maka kedua bidang dikatakan
berpotongan. Perpotongannya dinamakan garis potong atau garis tembus.
 |
| sumber: bangkusekolah.com |
g. Istilah-istilah pada Bangun Ruang
1. Bidang
Gambar
Bidang gambar
merupakan suatu bidang datar yang akan digunakan untuk menggambar bangun ruang. Pada kubus di bawah ini, bidang gambar ditunjukkan oleh bidang α yang dibatasi oleh warna biru.
 |
| Bidang gambar α |
2. Bidang
Frontal
Bidang frontal
adalah bidang yang terletak pada bidang gambar atau bidang yang sejajar bidang
gambar. Contoh bidang frontal adalah bidang sisi kubus yang letaknya di depan
atau di belakang.
 |
| Bidang frontal ABFE dan CDHG |
3. Bidang
Ortogonal
Bidang orthogonal
adalah bidang-bidang yang tegak lurus bidang frontal.
 |
| Bidang orthogonal ABCD, EFGH, BCFG, dan ADHE |
4. Garis
Frontal
Garis frontal
adalah garis-garis yang terletak pada bidang frontal. Ada dua jenis garis
frontal yaitu garis frontal horizontal (mendatar) dan vertikal (tegak). Pada kubus ABCD EFGH di bawah ini, garis frontal horizontalnya adalah AB, EF, CD, dan GH. Sedangkan, garis frontal vertikalnya adalah AE, BF, CG, dan DH.
5. Garis
Ortogonal
Garis orthogonal
adalah garis-garis pada bidang ortogonal yang tegak lurus bidang frontal.
Garis orthogonal dari kubus di bawah ini adalah AD, BC, EH, dan FG.
6. Perbandingan
Ortogonal
Perbandingan
ortogonal adalah perbandingan panjang garis ortogonal pada gambar dan panjang
garis ortogonal sebenarnya.
7. Sudut
Surut
Sudut surut yaitu
sudut antara garis frontal horizontal arah ke kanan dan garis ortogonal arah ke
belakang yang saling berpotongan. Perhatikan gambar berikut. Sudut surutnya adalah BAD dan FEH.
Baca juga: Logika matematika
B. Jarak pada Bangun Ruang
a. Garis Tegak Lurus Bidang
Terdapat beberapa
dalil yang berkaitan dengan suatu garis yang tegak lurus bidang.
1. Jika sebuah garis
tegak lurus pada sebuah bidang maka garis tersebut akan tegak lurus dengan
setiap garis yang terletak pada bidang itu.
2. Garis l tegak lurus bidang α apabila sedikitnya garis l tegak lurus dengan dua garis yang berpotongan
pada bidang α.
3. Jika salah satu
dari dua buah garis sejajar tegak lurus pada sebuah bidang maka garis lainnya
juga tegak lurus pada bidang itu.
b. Jarak Titik ke Titik Lain
Jarak antara dua titik merupakan panjang
garis yang menghubungkan kedua titik tersebut.
c. Jarak Titik ke Garis
Jarak antara titik dan garis merupakan
panjang garis yang ditarik dari titik tersebut hingga memotong garis secara
tegak lurus.
Contoh 1:
d. Jarak Titik ke Bidang
Jarak titik ke bidang merupakan panjang dari ruas garis yang ditarik dari suatu titik hingga memotong tegak lurus suatu
bidang.
Contoh 2:
e. Jarak antara Dua Garis
1. Jarak antara dua garis yang sejajar adalah panjang ruas garis yang ditarik dari suatu titik pada salah satu garis sejajar dan tegak lurus garis sejajar yang lain.
2. Jika kedua garis bersilangan maka jaraknya ditentukan dengan panjang ruas garis hubung yang letaknya tegak lurus pada kedua garis yang bersilangan itu.
f. Jarak antara Garis dan Bidang
Jarak antara titik dan garis yang sejajar
ditentukan dengan cara mencari jarak antara salah satu titik pada garis yang
tegak lurus terhadap bidang.
g. Jarak antara Dua Bidang
Jarak antara dua bidang yang sejajar sama
dengan jarak antara sebuah titik pada salah satu bidang ke titik pada bidang
lainnya yang saling tegak lurus.
Baca juga: Persamaan dan pertidaksamaan nilai mutlak
C. Sudut pada Bangun Ruang
Sebelum
membahas sudut pada bangun ruang, perlu dipahami terlebih dahulu tentang
proyeksi.
Terdapat
tiga kemungkinan proyeksi sebuah garis pada bidang yaitu:
1. Jika
garis l tegak lurus bidang α maka proyeksi l pada bidang α adalah titik.
2. Jika
garis l sejajar bidang α maka proyeksi l pada bidang α adalah sebuah garis yang sejajar dengan garis l.
3. Jika
garis l menembus bidang α maka proyeksi l pada bidang α ditentukan dengan cara:
a. cari
titik tembus garis l pada bidang α
b. titik
ujung garis l yang terletak di luar bidang α ditarik proyeksinya pada bidang α
c. selanjutnya
hubungkan titik tembus dengan hasil proyeksi titik ujung
a. Sudut antara Dua Garis Berpotongan dan Bersilangan
Secara umum, sudut dibentuk oleh dua garis
yang berpotongan. Jika kedua garis bersilangan maka besar sudut ditentukan
dengan membuat garis sejajar dengan salah satu garis bersilangan dan memotong
garis lain.
b. Sudut antara Garis dan Bidang
Sudut antara garis dan bidang
didefinisikan sebagai sudut yang antara garis tersebut dan proyeksi garis
tersebut pada bidang.
 |
| Ilustrasi sudut antara garis dan bidang |
Contoh 3:
Jika terdapat dua
bidang yang saling berpotongan maka besar sudut antara kedua bidang tersebut
ditentukan dengan langkah-langkah berikut ini:
- Tentukan
sebuah titik, misalkan titik A, pada garis potong kedua bidang.
- Melalui
A buatlah garis l yang terletak pada bidang α dan garis m yang terletak pada bidang β dimana garis l dan m keduanya tegak lurus garis potong.
- Sudut
antara dua bidang α dan β sama dengan sudut antara garis l dan m yaitu θ.
 |
| Ilustrasi sudut antara dua bidang yang berpotongan |
Tidak ada komentar:
Posting Komentar