Trigonometri

A. Perbandingan Trigonometri
Ada tiga perbandingan trigonometri dalam segitiga siku-siku yaitu sinus disingkat sin, cosinus disingkat cos dan tangens disingkat tan. 

Hipotenusa disebut juga dengan sisi miring. Sisi miring selalu berada di depan sudut siku-siku. 

Terdapat 3 perbandingan lain yang merupakan kebalikan dari tiga perbandingan di atas yaitu cosecan disingkat cosec, secan disingkat sec dan cotangent disingkat cotan.

B. Sudut dan Pengukurannya

Terdapat dua ukuran sudut yaitu derajat (°) dan radian (rad). 

1 radian adalah sudut yang dibentuk oleh dua jari-jari lingkaran yang berpusat di O dan panjang busur di depannya sama dengan panjang jari-jari lingkaran. Satu putaran penuh pada lingkaran sama dengan 360°. 

Contoh 1:

C. Nilai-Nilai dari Sudut Istimewa

Nilai-nilai fungsi trigonometri dari sudut-sudut istimewa disajikan dalam tabel berikut:

D. Perbandingan Trigonometri Suatu Sudut di Berbagai Kuadran

E. Sudut-Sudut Berelasi

Hubungan nilai perbandingan trigonometri sudut di berbagai kuadran dinyatakan sebagai berikut:

Aturan formulasi di atas adalah sebagai berikut:

1. Jika menggunakan 90° atau 270° maka nama fungsinya diubah.

sin menjadi cos; cos menjadi sin; tan menjadi cotan; sec menjadi cosec; cosec menjadi sec; cot menjadi cotan. 

2. Jika menggunakan 180° atau 360° maka nama fungsinya tetap sama. 

3. Tanda positif dan negatif ditentukan berdasarkan letak fungsi dalam kuadran.

Contoh 2:

Baca juga: Logika matematika

F. Identitas Trigonometri

G. Aturan Sinus, Kosinus, dan Luas Segitiga

Aturan sinus digunakan untuk menentukan unsur-unsur lain dalam suatu segitiga sebarang untuk dua kasus berikut:

1. Dua sudut dan satu sisi diketahui

2. Dua sisi dan satu sudut di depan salah satu sisi itu diketahui

Contoh 3:

Aturan kosinus digunakan untuk menentukan unsur-unsur lain dalam segitiga sebarang untuk dua kasus berikut:

1. Tiga sisi diketahui

2. Dua sisi dan sudut apitnya diketahui

Contoh 4:

Misalkan terdapat segitiga seperti gambar berikut:

Jika tidak diketahui tingginya maka luas segitiga tersebut dapat ditentukan dengan formulasi berikut ini.

1. Luas Segitiga dengan Besar Sudut dan Dua Sisi yang Mengapit Sudut itu Diketahui

2. Luas Segitiga dengan Besar Dua Sudut dan Satu Sisi yang Terletak di antara Kedua Sudut Diketahui

3. Luas Segitiga dengan Ketiga Sisinya Diketahui

Baca juga: Dimensi tiga

H. Persamaan Trigonometri

Perhatikanlah bentuk-bentuk dasar persamaan trigonometri beserta penyelesaiannya.

Contoh 5:

I. Rumus-Rumus Trigonometri

1. Rumus Jumlah dan Selisih Sudut

2. Rumus Trigonometri Sudut Ganda

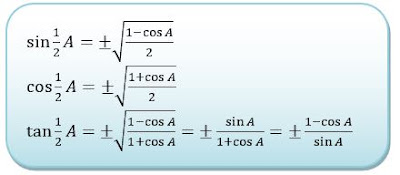
3. Rumus Trigonometri Setengah Sudut

4. Rumus Konversi Perkalian ke Penjumlahan/Pengurangan

5. Rumus Konversi Penjumlahan/Pengurangan ke Perkalian

Contoh 6:

Contoh 7:

Contoh 8:

Contoh 9:

Contoh 10: